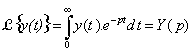
(2.25)
|
Obsah kapitoly: |
2.3.1 Definice a vlastnosti Laplaceovy transformace 2.3.2 Linearizace matematického modelu |
Laplaceova transformace je matematický nástroj, který je široce používán v teorii regulace. Umožňuje převádět za určitých podmínek diferenciální rovnice na algebraické a tím usnadňuje jejich řešení. Dlužno však říci, že význam Laplaceovy transformace jako prostředku k řešení diferenciálních rovnic s rozvojem výpočetní techniky a využívání simulačních nástrojů výrazně ustupuje do pozadí. V teorii regulace ale zůstává stále základním matematickým nástrojem, na němž jsou založeny metody popisu soustav, sledování stability regulačních obvodů, nastavování parametrů regulátorů apod. Proto se alespoň stručně zmíníme o její podstatě a možnostech využití.
2.3.1 Definice a vlastnosti Laplaceovy transformace
Laplaceova transformace je integrální transformace, která převádí funkci y(t) reálné proměnné t („předmět“) na funkci Y(p) obecně komplexního argumentu p („obraz“). Je definována vztahem
|
|
|
|
(2.25) |
a transformovaná funkce y(t) musí splňovat tyto podmínky:
| · je po částech spojitá, | |
| · je exponenciálního řádu, tj. |
|
| · musí pro ni platit, že je | y(t) = 0 pro t<0 |
Základní vlastnosti Laplaceovy transformace jsou:
|
a) |
linearita |
|
A, B ... konstanty |
(2.26) |
| b) | obraz derivace |
|
(2.27) | |
| c) | věta o konečné hodnotě |
|
(2.28) | |
| d) | násobení eat |
|
(2.29) |
Protože určování obrazů integrací podle definiční rovnice (2.25) je dost nepříjemné, byl vypracován slovník Laplaceovy transformace, kde jsou k často se vyskytujícím předmětům uvedeny odpovídající obrazy. Několik základních položek slovníku uvádíme v následující tabulce:
| předmět | název funkce | obraz |
|
Diracův impuls |
1 | |
|
jednotkový skok |
||
| t |
čas (nezávisle proměnná) |
|
| tn |
n-tá mocnina času (nezávisle proměnné) |
|
|
1.derivace (nulové počáteční podmínky) |
||
|
n-tá derivace (nulové počáteční podmínky |
||
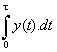 |
integrál (podle nezávisle proměnné) |
| na začátek kapitoly |
2.3.2 Linearizace matematického modelu
Všimněme si, že obraz derivace (rovnice 2.27) se výrazně zjednoduší, pokud jsou počáteční podmínky (tj. hodnota y v bodě 0, popřípadě hodnoty všech derivací y od y’ do y(n-1) v bodě 0) nulové. Pokud tomu tak není, ztrácí transformace svou velkou přednost. Proto se provádí před transformací úprava rovnic tak zvanou linearizací. Mějme např. matematický model nějakého systému daný rovnicemi
|
|
|
x(0) =x0 |
(2.30) |
|
y = g(x, u) |
Linearizaci provádíme vždy v okolí nějakého pracovního bodu, v našem případě (x0, y0, u0). Tímto pracovním bodem bývá nejčastěji ustálený stav, což pro náš model matematicky vyjádřeno znamená, že v pracovním bodě platí
|
|
|
y0 = g(x0, u0) |
(2.31) |
Při linearizaci postupujeme takto:
1. Zavedeme nové proměnné jako odchylky hodnot původních proměnných od jejich hodnot v pracovním bodě, tedy
|
|
Dx = x - x0 , Dy = y - y0 , Du = u - u0 |
|
2. Vyjádříme z těchto definic původní proměnné, dosadíme do modelových rovnic a provedeme příslušné matematické operace, přičemž zanedbáme součiny odchylek a případné nelineární funkce rozvineme v pracovním bodě do Taylorovy řady, v našem případě
|
|
|
|
(2.32) |
3. Po algebraických úpravách dostaneme linearizovaný matematický model, tedy
|
|
|
|
(2.33) |
|
|
Dy = C.Dx + D.Du |
||||
|
|
Tento model má již nulové počáteční podmínky, takže Laplaceova transformace derivací je jednoduchá. Je však třeba si uvědomit, že za zjednodušení platíme vnášením chyby, která je tím větší, čím větší jsou při práci s tímto modelem odchylky od pracovního bodu.
| na začátek kapitoly |
2.3.3 Přenosová funkce, algebra blokových schémat
Dosud jsme pracovali s matematickým popisem chování systému, tj. vztahu mezi vstupní funkcí u(t) a výstupní funkcí y(t), pomocí diferenciální rovnice. Často se však můžeme setkat (v teorii regulace běžně, ale i v chemickém inženýrství, analytické chemii a jinde) s vyjádřením chování systému pomocí tzv. přenosové funkce (podle staré normy „obrazového přenosu“). Ta je definována vztahem
|
|
|
|
(2.34) |
Z matematického hlediska je to algebraický výraz, nejčastěji ve tvaru polynom lomeno polynomem. Je třeba si uvědomit, že kolik vstupů do systému majících vztah k danému výstupu existuje, tolik přenosových funkcí musí být k popisu systému definováno. Schématicky se vyjadřuje systém jako blok charakterizovaný svou přenosovou funkcí:
|
|
Takto definované bloky můžeme libovolně spojovat (sériově, paralelně, kombinovaně,...) a přenosová funkce výsledné kombinace se jednoduše určí pomocí algebraických operací. Pro přenosové funkce základních kombinací platí:
| · | sériové zapojení bloků |
|
|
| · | paralelní zapojení bloků |
|
|
| · | antiparalelní zapojení bloků (v záporné zpětné vazbě) |
|
|
Výhodou algebry blokových schémat je, že můžeme vytvářet v podstatě libovolné systémy vzájemným propojováním dílčích (stavebnicových) bloků a poměrně jednoduchým výpočtem určovat jejich výslednou přenosovou funkci.
| na začátek kapitoly |
Příklad L-1
Úkol:
Matematický model pro výšku hladiny v nádrži s proměnným přítokem a s výtokem řízeným ventilem (viz příklad M-3) je popsán diferenciální rovnicí
|
|
|
Hodnota hladiny h0 odpovídá ustálenému stavu.
Simulace:
V následujícím simulačním programu je paralelně řešen linearizovaný i nelinearizovaný model. Aby bylo možné použít demoverze PSI, musel být počet bloků redukován, proto jsou použity číselné konstanty přímo v rovnicích. Hodnoty parametrů modelu jsou: A = 3 dm2, k = 6.88, pro ustálený stav jsou Q10 = 10 l.min-1, x0 = 0.65, h0 = 5 dm. Doba simulace je 30 minut, změny vstupů jsou v programu realizovány změnami hodnot konstant dQ a dx v programu. K numerickému řešení je použito metody Runge-Kutta 2.řádu, krok výpočtu je 0,001.
| Výpis programu: |
% Příklad L-1 (ukázka vlivu linearizace na přesnost modelu) % rovnice pro hladinu bez linearizace h = INT((Q1-6.88*x*sqrt(h))/3 PAR: 5); % (dm) % rovnice pro odchylku hladiny (po linearizaci) dh = INT((dQ1-6.88*(k1*dx+k2*dh))/3 PAR: 0); % (dm) hlin= 5+dh; % přepočet odchylky na abs.hodnotu výšky hladiny % konstanty linearizovaného modelu k1 = sqrt(5); k2 = 0.65/(2*sqrt(5)); % vstupní veličiny dQ1 = 0; % změna přítoku (l/min) dx = 0.0; % změna stupně otevření ventilu (1) Q1 = 10+dQ1; x = 0.65+dx; |
| Ukázka výsledků:
odezva na DQ = 2 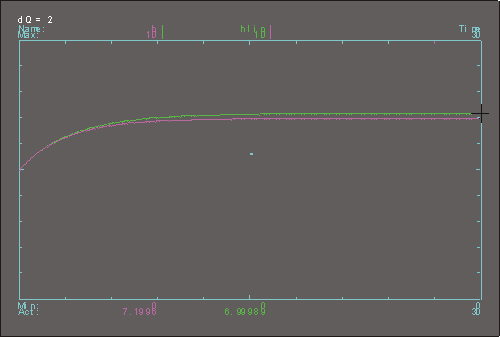
|
|
|
odezva na Dx = 0.2
|
|
|
Program v PSI: |
soubory: Prikl_L-1.PSM , Prikl_L-1.MOD |
U dolního okraje grafů jsou znázorněny číselné hodnoty výstupu obou modelů po 30 minutách simulace. Je vidět, že rozdíl nových prakticky ustálených hodnot mezi linearizovaným a nelinearizovaným modelem není zanedbatelný, zvláště v případě odezvy na změnu stupně otevření ventilu.
| na začátek kapitoly |