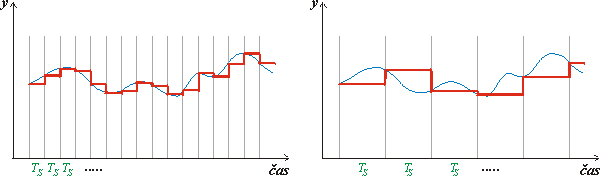
Obr. 3.30 Ukázka výsledku vzorkování signálu s různou periodou TS
3.7 Nespojité regulační obvody
|
Obsah kapitoly: |
3.7.1 Číslicové zpracování signálu |
Využívání počítačové techniky v řízení procesů znamenalo přechod od analogových, spojitě pracujících přístrojů k číslicovým, které ze své podstaty pracují nespojitě. V souvislosti s tím se objevily některé nové problémy, které bylo nutno řešit.
3.7.1 Číslicové zpracování signálu
Prvním problémem je, že výpočetní technika vyžaduje informace ve formě čísel, takže spojitý signál z technologického procesu je třeba převést na číslicový. Provádí se to tak, že se hodnoty měřených veličin snímají v určitých časových intervalech; hovoříme o tzv. vzorkování signálu. Jeho princip je znázorněn na obr. 3.30. Je vidět, že z původního spojitého signálu (modrá křivka) dostaneme signál, jehož časový průběh je stupňovitý (červená čára). Je také zřejmé, že průběh a tím i vypovídací úroveň číslicového signálu bude záviset na periodě vzorkování TS . V pravé části obrázku je perioda vzorkování trojnásobná oproti části levé a výsledný číslicový signál už původní průběh příliš dobře nevystihuje.
|
|
|
Obr. 3.30 Ukázka výsledku vzorkování signálu s různou periodou TS |
Vzhledem k současné vysoké rychlosti řídicích počítačů mohou být tyto časové intervaly velice krátké, takže se signál prakticky blíží spojitému. Je ale třeba si uvědomit, že v časové prodlevě mezi jednotlivými vzorky nemá řídicí systém o řízené soustavě žádnou informaci a nemůže tedy reagovat na změnu jejího stavu. Perioda vzorkování musí být proto volena s ohledem na rychlost průběhu (hodnoty časových konstant) řízeného procesu. Pro periodu vzorkování musí platit vztah (tzv. vzorkovací teorém)
|
|
|
|
(3.10) |
kde TS je perioda vzorkování, Tmin nejmenší perioda signálu, kterou chceme podchytit, respektive fmin. nejvyšší frekvence obsažená v signálu, který chceme sledovat. V praxi se však doporučuje volit periodu vzorkování dvakrát až pětkrát menší než vychází z rovnice (3.10).
| na začátek kapitoly |
Spojité regulátory PID se v praxi natolik osvědčily, že realizace jejich funkcí byla převedena i do číslicových algoritmů a běžně se při počítačovém řízení využívá. Při převodu funkcí byly spojité operace (integrace, derivace) nahrazeny numerickými formulemi. Ukážeme si to na příkladu matematického popisu funkce regulátoru PI s interakcí:
|
|
|
|
(3.11) |
Jestliže tuto rovnici převedeme do přírůstkového tvaru (tj. vyjádříme velikost změny výstupu z regulátoru za periodu vzorkování)a upravíme na rozdíly proporcionální části a integrační části zvlášť, dostaneme
|
|
|
|
a po náhradě integrace numericky (obdélníkovým pravidlem) a zavedení indexování pro čas (čas t ... index k, čas t-TS ... index k-1) dostaneme
|
|
|
|
(3.12) |
což je číslicový ekvivalent rovnice (3.11).
Obdobným způsobem můžeme odvodit i algoritmus pro číslicovou variantu regulátoru PID (nazývá se někdy PSD) a v tzv. přírůstkové formě (určuje změnu akční veličiny oproti minulému kroku) má tvar:
|
|
|
|
(3.13) |
kde platí následující relace mezi konstantami číslicové a analogové verze (TS je perioda spouštění číslicového regulátoru):
|
|
|
|
(3.14) |
|
|
|||
|
|
Je třeba si uvědomit, že vlastně přibyl další parametr regulátoru, protože akční zásah nezávisí jen na hodnotách zesílení a časové integrační konstanty, ale také na velikosti periody vzorkování.
Číslicový regulátor funguje tak, že v okamžiku vzorkování sejme hodnotu regulované veličiny, vypočte akční zásah (např. podle 3.12), nastaví výstupní signál do procesu na odpovídající hodnotu a tu udržuje po celou dobu periody vzorkování konstantní. Změní ji až po novém sejmutí hodnoty regulované veličiny a výpočtu nového akčního zásahu. Ukázka záznamu regulačního pochodu číslicového regulátoru je na obr. 3.31. V horní části obrázku je červeně průběh vzorkované regulační odchylky a v dolní fialově průběh akčního zásahu. Pro porovnání je modře vynesen i spojitý průběh regulační odchylky.
|
|
|
Obr. 3.31 Záznam regulačního pochodu s číslicovým regulátorem |
Moderní mikropočítačové regulátory pracují s velmi krátkou periodou vzorkování (řádově jednotky až stovky milisekund), takže vůči běžně rychlým dějům se vlastně chovají jako spojité.
| na začátek kapitoly |
3.7.3 Číslicová filtrace signálu
Měřené signály bývají v praxi často zhoršeny tzv. šumem, tj. náhodným rušivým signálem o frekvenci vyšší než je frekvence užitečného signálu. Tento šum se s měřeným signálem sčítá. Je-li šum velký, je signál nepoužitelný k řízení, ale i menší šum může způsobovat při vzorkování zkreslení informace tak, že řídicí systém na ně reaguje a vnáší do procesu nežádoucí zásahy.
Na následujícím obrázku 3.32 je názorně vidět, jak ke zkreslení může docházet. Černá křivka znázorňuje signál bez šumu, ale snímač dává zašuměný signál, což představuje modrá křivka. Tento signál je pak vzorkován a je vidět, že získaná informace (červeně) původní správný signál (bez šumu) příliš nevystihuje.
|
|
|
Obr. 3.32 Zkreslení signálu šumem a vzorkováním |
Takto zkreslené signály lze při číslicovém zpracování zlepšit tzv. číslicovou filtrací. Číslicová filtrace tvoří samostatnou rozsáhlou oblast v metodice zpracování signálů a podrobnější výklad by přesahoval rozsah tohoto předmětu. Uvedeme zde pouze jednoduchý filtr pro potlačení signálů o vyšších frekvencích, který je matematicky popsán diferenciální rovnicí soustavy 1.řádu
|
|
|
yM
... měřená hodnota, |
(3.15) |
Jestliže derivaci v této rovnici nahradíme přibližným vztahem DyF/Dt , kde Dt = TS, dostaneme po úpravě vztah pro tzv. exponenciální filtr
|
|
|
|
(3.16) |
kde je: yFn
... nová filtrovaná hodnota (v aktuálním čase t), yFs
... filtrovaná hodnota o periodu zpět (v čase
t-TS),
yM ...
měřená hodnota,
KF
... koeficient filtrace
Hodnota KF se volí podle účelu, ke kterému se filtrovaný signál využívá, např. pro číslicové regulátory se volí v rozmezí 0.4 až 0.6 , pro adaptivní řízení, které má reagovat jen na dlouhodobé změny, se volí kolem 0.01 . V konkrétním případě je nejlépe vhodnou hodnotu vyzkoušet.
Jako další běžně používané filtry uvedeme ještě dva:
· mediánový filtr jako filtrovanou hodnotu bere medián (prostřední hodnotu při seřazení podle velikosti) ze tří nebo pěti naposled sejmutých hodnot a je vhodný pro eliminaci náhlých velkých odchylek měřené hodnoty.
· filtrace klouzavým průměrem se provádí tak, že se jako filtrovaná hodnota bere aritmetický průměr určitého počtu naposled změřených hodnot. Používá se tam, kde potřebujeme u signálu sledovat spíše jeho dlouhodobější trendy než krátkodobé změny a podle toho také volíme počet průměrovaných hodnot.
| na začátek kapitoly |
3.7.4 Ukázky simulace nespojitých obvodů
Ukázka R-6
Úkol:
Vytvořit simulační program, který umožní vzorkovat signál sinusového průběhu s různou periodou.
Řešení:
Funkci sinus generujeme zabudovanou funkcí, jako argument použijeme t.2p/T, kde T je perioda kmitů. Pro vzorkování je použit blok VRZ, který vzorkuje vstupní signál s periodou určenou nastavením příslušného časovače (Timer), časovač se nastavuje z menu Data / Timers.
| Výpis programu: |
% Ukázka R-6 (vzorkování signálu) % generování fce sinus T = 5; % perioda kmitů funkce sinus y = 1.5+sin(time*2*PI/T); % vzorkování y periodou Ts yvz1 = VRZ(y PAR:1); % per.vzorkování podle Timer 1 |
| Ukázka výsledků:
perioda vzorkování TS = 0.5, což je desetina periody vzorkované funkce; výsledek je celkem uspokojivý
|
|
|
perioda vzorkování TS = 1.25, což je čtvrtina periody vzorkované funkce; výsledek je špatný, i když podmínka daná rovnicí (3.10) je splněna
|
|
|
Program v PSI: |
soubory: Ukaz_R-6.PSM , Ukaz_R-6.MOD |
| na začátek kapitoly |
Ukázka R-7
Úkol:
Vytvořit simulační program pro regulaci teploty v ohřívači (viz ukázka R-4) číslicovým PI regulátorem (blok PIZ).
Řešení:
Model
soustavy je stejný s ukázkou R-4, stejné jsou i omezení výstupu z regulátoru
a ovládání topení. Informace o teplotě se ale získává vzorkováním
(T2vz) s periodou danou časovačem Timer 1. Regulátor pracuje podle
rovnice (3.12), jeho konstanty jsou:
KP = r0
(zesílení, 3.parametr bloku PIZ),
Ki = r0.TS / Ti
(integrační konstanta, 4.parametr bloku PIZ).
| Výpis programu: |
% Ukázka R-7 (číslicová regulace teploty na výstupu ohřívače vody) % regulovaná soustava T2 = INT((Q*(15-T2)+P*k)/5 PAR:40); % teplota na výstupu T2vz= VRZ(T2 PAR: 1); % vzorkování reg.vel. k = 2.388e-4; % konstanta k P = v*100000; % ovládání příkonu topení regulátorem Q = BNG(time PAR:0.5,0.4,5); % porucha - skok průtoku vody % číslicový regulátor Tw = 40; % žádaná hodnota teploty e = Tw-T2vz; % regulační odchylka vreg= PIZ(e PAR: 0.523,1,0.2,0.18); % číslicový regulátor PI v = LIM(vreg PAR:0,1,1); % omezení výstupu regulátoru |
| Ukázka výsledků:
perioda vzorkování TS =0.5
|
|
|
Program v PSI: |
soubory: Ukaz_R-7.PSM , Ukaz_R-7.MOD |
| na začátek kapitoly |
Ukázka R-8
Úkol:
Vytvořit simulační program, který umožní vzorkovat zašuměný signál a filtrovat jej exponenciálním filtrem.
Řešení:
Základní signál je generován z tabulky taby pomocí bloku FNG a k němu je přičten šum vytvořený blokem NOI. Takto zašuměný signál je jednak vzorkován bez filtrace (yvz), jednak vzorkován a filtrován exponenciálním filtrem (yF) podle rovnice (3.16). Je možné zkoušet vliv filtrační konstanty a periody vzorkování na průběhy signálů.
| Výpis programu: |
% Ukázka R-8 (filtrace zašuměného signálu) y = FNG(time PAR:0,10,2,taby); % původní signál sum = NOI(PAR:0,0.05,2); % generátor šumu ysum = y+sum; % zašuměný signál yvz = VRZ(ysum PAR:1); % vzorkovaný signál bez filtrace % číslicový exponenciální filtr yFs = ZZZ(yf PAR:0.3,1); % uložení yf pro příští vzorek yF = VRZ(KF*ysum+(1-KF)*yFs PAR:1); % vzorkovaný signál s filtrací KF = 0.5; % filtrační konstanta |
| Ukázka výsledků:
perioda vzorkování TS = 0.2 , filtrační konstanta KF = 0.5
|
|
|
perioda vzorkování TS = 0.2 , iltrační konstanta KF = 0.1
|
|
|
Program v PSI: |
soubory: Ukaz_R-8.PSM , Ukaz_R-8.MOD |
| na začátek kapitoly |