PSI manuál

P1.2 Bloky (funkce) jazyka PSI

Dynamické spojité	DIF	INF	INT	PIC	TDE
Dynamické diskrétní	TIM	SPL	PIZ	VRZ	ZZZ
Logické	COUNT	FFL	PWM
Nelineární	BNG	FNG	FNG2	HYS	LIM	MON	QUANT
Pomocné	CON	GEN	GAIN	NOI	PAR	RELAY	VAR

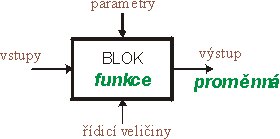
OBECNÉ SCHÉMA BLOKU:

(počáteční podmínky a řídicí veličiny tvoří tzv. parametry bloku)

*funkce*	identifikátor označující typ bloku a tím jeho funkci
	(viz seznam funkcí jazyka)
*proměnná*	identifikátor volený uživatelem
	označuje výstup z bloku (v matematickém popisu funkce bloků je označována jako y )
vstupy	značeny i₁, i₂, ...
	jsou to proměnné nebo aritmetické výrazy
parametry	značeny p₁, p₂, ...
	mohou jimi být pouze konstanty nebo jednoduché proměnné, nemohou jimi být aritmetické výrazy
a)	počáteční podmínky: určují počáteční stav modelu; mohou jimi být hodnoty konstant nebo jednoduché
	proměnné (výstupy bloku PAR)
b)	řídicí veličiny: řídí chování bloku, mohou jimi být konstanty (p₁, p₂,...) i proměnné (i₁, i₂,...)

ZÁPIS PŘÍKAZU:

proměnná = funkce ( i₁, i₂ ,... PAR: p₁, p₂, ... ) ;

(oddělovačem je čárka, před PAR je mezera, na konci příkazu musí být středník)

VYBRANÉ BLOKY (FUNKCE)

Z funkcí jazyka PSI jsou zde popsány jen ty, které jsou univerzálně použitelné v úlohách, kterými se budeme zabývat. Jsou uvedeny v abecedním pořádku. Všechny existující bloky jazyka PSI jsou popsány v nápovědě, která je součástí programu.

BNG	přepínač "bang-bang" (změna hodnoty konstanty podle řídicí proměnné)
	y = BNG (i₁ PAR: p₁, p₂, p₃);

	y = p₁	pro i₁ < p₃
	y = p₂	pro i₁ ł p₃

CON	konstanta
	y = CON ( PAR: p₁) ;

y = p₁

Poznámka: V aritmetických výrazech je možné používat zápisu číselné konstanty přímo, tohoto bloku se používá pouze tehdy, když je třeba téže konstanty buď používat na více místech, nebo jako optimalizačního parametru a nebo když má být viditelně oddělena od ostatních příkazů modelu. Je možný i zápis

y = konstanta;

COUNT

čítač (slouží k počítání pulsů)

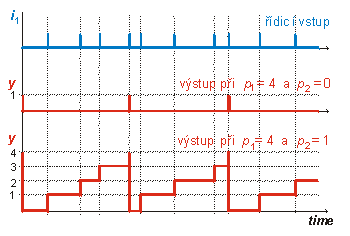
y = COUNT (i₁, i₂ PAR: p₁, p₂) ;

i₁ ... vstup pulsů, které mají být počítány

i₂ ... řídicí vstup: je-li i₂ > 0, je čítač vynulován a y = 0

p₁ ... předvolba ( p₁ ł 1)

p₂ ... řídicí parametr:

p₂ = 0:

výstup y = 1, 0, 0, ..., 1, 0, 0, ...

tj. výstup y je stále 0, pouze když počet pulsů je právě roven p₁, tak je y =1

p₂ = 1:

výstup y = p₁, 0, 1, 2, ..., p₁, 0, 1, 2, ...

tj. výstup y je na počátku roven předvolbě p₁, ale je ihned vynulován, pak se každým pulsem zvětšuje o 1 a po dosažení předvolby p₁ je opět vynulován, atd.

DIF	numerická derivace
	y = DIF(i₁PAR: p₁) ;

p₁= i₁(-T)

T ... výpočetní krok nezávisle proměnné ("integration interval"),

t ... okamžitá hodnota nezávisle proměnné (TIME)

FFL	RS klopný obvod ("flip flop")
	y = FFL(i₁, i₂, i₃PAR: p₁, p₂);

	i₁ ... řídicí vstup:	i₁ Ł 0 ... RS obvod funguje podle předpisu i₁ > 0 ... obvod vyřazen, y_k = y_k-1
	i₂ ... nulovací vstup (R) :	i₂ > 0 => y_k = 0
	i₃ ... nastavovací vstup (S) :	i₃ > 0 => y_k = 1
	i₂ Ł 0 a zároveň i₃ Ł 0 => y_k = y_k-1 (pro nestandardní případ: i₂> 0 a zároveň i₃> 0	=> y_k = p₂
	p₁ = y(0) (počáteční hodnota výstupu) ,	0 Ł p₁ Ł 1
	p₂... hodnota výstupu pro R=1 a zároveň S=1,	0 Ł p₂ Ł 1

FNG	generátor funkce jedné proměnné dané tabulkou
	y = FNG (i₁PAR: p₁, p₂, p₃, p₄);

y = f (i₁)

tabulka musí být v nezávisle proměnné dělena ekvidistantně,

p₁ ... hodnota nezávisle proměnné odpovídající prvnímu bodu tabulky,

p₂ ... hodnota nezávisle proměnné odpovídající poslednímu bodu tabulky,

p₁Ł i₁ Ł p₂

p₃ ... řídicí parametr interpolace: p₃ = 1 ... lineární, p₃ = 2 ... kvadratická

p₄... jméno (identifikátor) tabulky, které jí uživatel přidělí při jejím vytváření

FNG2	generátor funkce dvou proměnných dané tabulkou
	y = FNG2 (i₁, i₂PAR: p₁, p₂, p₃, p₄, p₅);

y = f (i₁, i₂)

tabulka musí být v obou nezávisle proměnných dělena ekvidistantně, interpolace se provádí pouze lineární

p₁, p₂... dolní a horní mez první nezávisle proměnné v tabulce, p₁ Ł i₁ Ł p₂

p₃, p₄... dolní a horní mez druhé nezávisle proměnné v tabulce, p₃ Ł i₂ Ł p₄

p₅ ... jméno (identifikátor) tabulky, které jí uživatel přidělí při jejím vytváření

GAIN	násobení konstantou
	y = GAIN (i₁, PAR: p₁);
	y = p₁ . i₁

Poznámka: V aritmetických výrazech je možné používat zápisu číselné konstanty přímo.

GEN

generátor šesti standardních signálů

y = GEN (PAR: p₁, p₂, p₃, p₄, p₅, p₆);

p₁ = y(0)

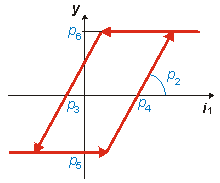
HYS	hystereze signálu
	y = HYS ( i₁ PAR: p₁, p₂, p₃, p₄, p₅, p₆) ;

p₁ = y(0)

p₂ > 0 směrnice přechodu z p₅ na p₆ a zpět

p₅Ł p₁Ł p₆

p₃< p₄

INF	soustava 1.řádu (soustava se zpožděním 1.řádu)
	y = INF ( i₁ PAR: p₁, p₂, p₃)

výstup je řešením diferenciální rovnice

p₁ = y(0),

p₂ = K (zesílení) ,

p₃ = t ą 0 (časová konstanta)

INT	integrace (numerická)
	y = INT ( i₁ PAR: p₁) ;

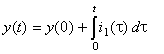p₁ = y(0)

t ... okamžitá hodnota nezávisle proměnné simulace (času)

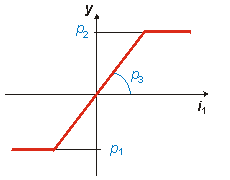
LIM	omezovač signálu (limiter)
	y = LIM ( i₁ PAR: p₁, p₂, p₃);

y = max ( min ( p₃ . i₁, p₂) , p₁)

p₁ Ł p₂

p₃ > 0 směrnice (zesílení limiteru)

MON	Monodova rovnice (resp. rovnice Michaelis - Mentenové)
	y = MON ( i₁ PAR: p₁, p₂);

p₁ ... 1.parametr (max.rychlost apod.)

p₂ ... 2.parametr (Michaelisova konstanta apod.)

NOI	generátor šumu (náhodného signálu)
	y = NOI ( PAR: p₁, p₂, p₃);

p₁, p₂ určují rozsah výstupu

p₃ určuje vlastnosti šumu:

p₃ = 1: rovnoměrné rozdělení amplitudy mezi p₁ a p₂

p₁ Ł p₂

p₃ = 2 : Gaussovo normální rozdělení amplitudy se střední hodnotou p₁a směrodat. odchylkou p₂

p₂ > 0

PAR	výpočet hodnoty konstanty ze vstupu i₁ v čase TIME = 0, identifikátor odpovídající y pak lze použít jako parametr bloků
	y = PAR ( i₁);

Poznámka: Tohoto bloku se doporučuje používat při optimalizaci pro definování optimalizačních parametrů.

PIC	spojitý regulátor PI
	y = PIC ( i₁ PAR: p₁, p_2,p₃);

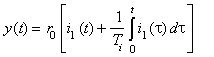i₁... regulační odchylka,

t ... okamžitá hodnota nezávisle proměnné

	p₁ = y(0) - r₀ . i₁(0)	(výstup pro TIME = 0 ),
	p₂ = r₀	(zesílení),
	p₃ = T_i > 0	(časová integrační konstanta)

PIZ	číslicový regulátor
	y = PIZ ( i₁ PAR: p₁, p₂, p₃, p₄);

y_k = y_k-1 + K_P [(i₁)_k - (i₁)_k-1] + K_I(i₁)_k

i₁ ... regulační odchylka

p₁ ... počáteční výstup: p₁ = y(0) - (K_P + K_I) . i₁(0)

p₂ ... číslo řídicího časovače (dává impulsy s periodou T_S)

p₃ ... konstanta K_P (proporcionální)

p₄ ... konstanta K_I (integrační)

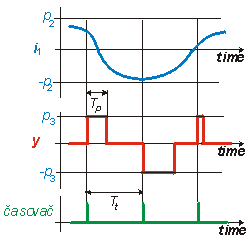
PWM	generátor pravidelných pulsů, jejichž šířka je určována vstupním signálem
	y = PWM ( i₁ PAR: p₁, p₂, p₃);

i₁ ... řídicí (modulační) signál

p₁ ... číslo časovače určujícího periodu pulsů

p₂ ... maximální šířka pulsu

p₃ ... maximální amplituda pulsu

Šířka pulsu se počítá z řídicího signálu podle vztahu

T_t ... perioda pulsů

QUANT	kvantovač
	y = QUANT (i₁ PAR: p₁, p₂, p₃);

	y = INTEGER (( p₁.i₁+ p₂ ) / p₃)
	p₃ nesmí být nulové

RELAY	přepínač signálů (relé)
	y = RELAY ( i₁, i₂ , i₃);

	i₁... řídicí vstup:	y = i₂	pro i₁ Ł 0
		y = i₃	pro i₁ > 0

SPL	vzorkovač
	y = SPL( i₁, i₂PAR: p₁);

	p₁ = y(0)
	i₁... řídicí vstup	y(k+1) = y(k) pro i₁(k+1) Ł 0 y(k+1) = i₂(k+1) pro i₁(k+1) > 0 (k ... index odpovídající čas.kroku řešení)

TDE	mrtvá doba (dopravní zpoždění)
	y = TDE( i₁ PAR: p₁, p₂, p₃);

y(t) = i₁(t - p₃) pro t ł p₃, t ... čas (TIME)

y(t) = p₁pro t < p₃

p₁ = y(0)

p₂ ... číslo časovače s periodou T_tim,

T_timł T (T...výpočetní krok simulace)

p₃ ... velikost dopravního zpoždění

TIM	časovač
	y = TIM( i₁ PAR: p₁);

p₁ ... číslo časovače

(1 Ł p₁ Ł max.počet časovačů v dané verzi PSI)

y ... sekvence impulsů o amplitudě 1 a s periodou danou časovačem číslo p₁ ;

výstup je aktivní pouze je-li i₁ > 0 , jinak je trvale y = 0

VAR	určení okamžité hodnoty spojité proměnné z okamžité hodnoty vstupu i₁
	y = VAR ( i₁) ;

Poznámka: Možný (a vzhledem ke zvyklostem z matematiky příjemnější) zápis proměnné je

y = výraz ;

VRZ	určení hodnoty diskrétní (nespojité) proměnné z okamžité hodnoty vstupu i₁
	y = VRZ ( i₁ PAR: p₁) ;

p₁ ... číslo časovače

(1 Ł p₁ Ł max.počet časovačů v dané verzi PSI)

i₁... spojitý vstup

y(t) = i₁(j)

(j ... čas odpovídající okamžiku posledního pulsu časovače)

ZZZ	dynamická paměť pro nespojité modely; zpoždění vstupu o jednu periodu danou časovačem
	y = ZZZ ( i₁ PAR: p₁, p₂) ;

p₁ = y(0) počáteční hodnota výstupu

p₂ ... číslo časovače určujícího periodu T

(1 Ł p₁ Ł max.počet časovačů v dané verzi PSI)

i₁... vstup

y(t) = i₁(t - T)