namísto příkazu
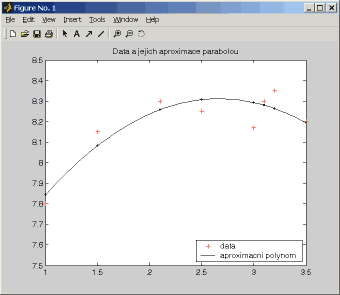
>> plot(u,v_aprox,'k.-') by se graf polynomu mohl vykreslit s menším krokem (bude vypadat lépe), například:>> plot(min(u):0.05:max(u),polyval(p,min(u):0.05:max(u)),'k',u,v_aprox,'k.')A výsledek:
V zimním semestru jsme se naučili používat funkci LINREGRESE (resp. LINEST v anglické verzi Excelu), která pomocí metody nejmenších čtverců vypočítala koeficienty přímky (y = m1x1 + m2x2 + ... + b), která nejlépe odpovídala zadaným datům (y, x1, x2...). Kromě vypočtených koeficientů funkce uměla vracet i další regresní statistiky. V MATLABu lze samozřejmě data aproximovat také. V případě, že chceme zadaná (naměřená) data aproximovat polynomem n-tého stupně, můžeme to jednoduše provést pomocí funkce polyfit, která používá metodu nejmenších čtverců:
p=polyfit(x,y,n), kde
x je vektor hodnot nezávisle proměnné,
y je vektor hodnot závisle proměnné,
n je stupeň polynomu, jímž chceme aproximovat body [xi,yi] a
p je vektor koeficientů výsledného polynomu P(x), přičemž P(x)=p(1)xn + p(2)xn-1 + ... + p(n)x + p(n+1)
Poznámky:
polyfit hlásí "Warning"
polyfit upravit (a uložit pod jiným názvem) nebo použít metodu nejmenších čtverců, která vede k řešení soustavy lineárních rovnic. Uvedené postupy lze samozřejmě použít pouze pro modely, které jsou lineární v parametrech!
Protože nás kromě koeficientů aproximačního polynomu většinou zajímají také hodnoty polynomu P(x) ve všech prvcích vektoru x (např. kvůli grafickému znázornění), existuje také funkce polyval:
y_aprox=polyval(p,x), kde
p je vektor koeficientů aproximačního polynomu,
x je vektor hodnot nezávisle proměnné a
y_aprox je vektor hodnot aproximačního polynomu.
Součet čtverců odchylek pak vypočteme snadno - buď pomocí cyklu for (přes všechny prvky y_aprox a y), anebo jednoduše s využitím toho, že nás zajímá součet prvků vektoru, který vznikl umocněním každého prvku vektoru rozdílů mezi y_aprox a y:
S=sum((y_aprox-y).^2)
Příklad - chceme aproximovat 8 naměřených hodnot u a v polynomem 2. stupně:
>> u=[1 1.5 2.1 2.5 3 3.1 3.2 3.5]; % namerena data, nezav. prom.
>> v=[7.8 8.15 8.3 8.25 8.1 8.3 8.35 8.2]; % namerena data, zav. prom.
>> p=polyfit(u,v,2) % koeficienty polynomu 2. stupne pro 'u' a 'v'
p =
-0.1684 0.8977 7.1150
>> v_aprox=polyval(p,u); % hodnoty polynomu v 'u'
>> S=sum((v_aprox-v).^2) % soucet ctvercu odchylek
S =
0.0345
>> plot(u,v,'r+') % graf, puvodni data jako cervene krizky
>> hold on % prikreslime dalsi
>> plot(u,v_aprox,'k.-') % graf polynomu jako cerne body spojene carou
>> axis([0.8 3.7 7.7 8.4]) % uprava os
>> title('Data a jejich aproximace parabolou')% nazev grafu
>> legend('data','aproximacni polynom',4) % zobrazime legendu (4 = vpravo dole)
A výsledek: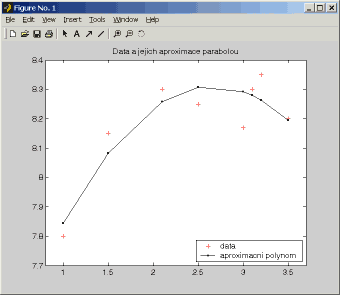
Samozřejmě by bylo lepší napsat tyto příkazy jako skript nebo ještě lépe jako funkci (aby se stupeň aproximačního polynomu dal snadno měnit).
Návrh na vylepšení:
namísto příkazu >> plot(u,v_aprox,'k.-') by se graf polynomu mohl vykreslit s menším krokem (bude vypadat lépe), například:
>> plot(min(u):0.05:max(u),polyval(p,min(u):0.05:max(u)),'k',u,v_aprox,'k.')
A výsledek:

Pokud chceme data aproximovat jinou funkcí než polynomem (např. f(x)=C1.sin(x)+C2.1/x), řešíme danou úlohu pomocí metody nejmenších čtverců (pouze pro modely, které jsou lineární v parametrech!), kdy pro neznámé koeficienty (C1, C2) získáme soustavu lineárních rovnic.