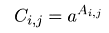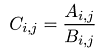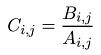a) unární
| název | syntaxe | popis | vyzkoušejte |
| unární plus | +a1 | - výsledek je shodný s a1 | >> +u |
| unární minus | -a1 | - výsledek je téhož rozměru jako a1 a obsahuje opačná čísla | >> -u |
| transpozice a konjugovanost | a1' | - výsledkem je transponovaná matice, přičemž všechna komplexní čísla změní znaménko imaginární části (na opačné) - u reálných matic funguje stejně jako .' | >> G' |
| transpozice | a1.' | - výsledkem je transponovaná matice (oproti ' nemění komplexní prvky znaménko imaginární části) | >> G.' |
b) binární
!!! POZOR u čtvercových matic !!!
Pro čtvercové matice většina operátorů funguje, aniž by MATLAB hlásil chybné rozměry matic. Proto je potřeba dávat si u těchto matic velký pozor na to, zda chceme provést operaci maticovou, anebo po prvcích. Výsledky jsou obecně odlišné!
Porovnejte např. výsledky následujících výrazů:
>> E*F
>> E.*F
>> F^3
>> F.^3
c) dvojtečka
| název | syntaxe | popis | vyzkoušejte |
| vytváření aritmetických posloupností | i:k:j | - všechny argumenty musí být SKALÁRY - vytvoří aritmetickou posloupnost od i do j s krokem k, tj. [i i+k i+2k ... j] (v případě, že (j-i)/k není celé číslo, tak poslední člen není j, ale číslo menší (maximálně o k-1))- není-li k použito, je krok automaticky volen jako jedna, tedy i:j generuje posloupnost [i i+1 i+2 ... j]- je-li krok zvolen chybně (nelze se od i dostat k j), pak je výsledkem prázdná matice | >> 1:3:10 |
2) Relační operátory
| název | syntaxe | popis | vyzkoušejte |
| menší | a1<a2 | - provádějí se po prvcích - argumenty musí mít STEJNÉ rozměry nebo alespoň jeden z nich je skalár - výsledek má rozměr jako neskalární argument (nebo je to skalár) - výsledek obsahuje pouze nuly (nepravda, false) a jedničky (pravda, true) podle toho, zda je příslušná relace mezi argumenty pravdivá - pokud je jeden z argumentů skalár, porovnává se s ním každý prvek druhého argumentu | >> A<3 |
| menší nebo rovno | a1<=a2 | ||
| větší | a1>a2 | ||
| větší nebo rovno | a1>=a2 | ||
| rovnost (je rovno?) | a1==a2 | ||
| nerovnost (je různé?) | a1~=a2 |
!!! POZOR: je velký rozdíl mezi == a = !!!
- v případě
x==5jde o výraz, jehož hodnotou je 0 nebo 1 (porovnáníxs číslem 5) axse nemění, zatímco
- v případě
x=5jde o přiřazení (příkaz), které nevrací hodnotu, nýbrž změní obsah proměnnéx!!!
3) Logické operátory
a) unární
| název | syntaxe | popis | vyzkoušejte |
| negace | ~a1 | - aplikuje se na každý prvek a1- výsledek má rozměr jako a1- výsledek obsahuje pouze nuly a jedničky (viz tabulka negace) | >> ~3.125 |
| negace | |
|---|---|
a1 | ~a1 |
| nenulové | 0 |
0 | 1 |
b) binární
| název | syntaxe | popis | vyzkoušejte |
| logický součin, AND | a1&a2 | - provádějí se po prvcích - argumenty musí mít STEJNÉ rozměry nebo alespoň jeden z nich je skalár - výsledek má rozměr jako neskalární argument (nebo je to skalár) - výsledek obsahuje pouze nuly a jedničky (viz tabulka logického součinu a součtu) |
>> A&D |
| logický součet, OR | a1|a2 |
>> A|D |
| logický součin a součet | |||
|---|---|---|---|
a1 | a2 | a1&a2 | a1|a2 |
| nenulové | nenulové | 1 | 1 |
| nenulové | 0 | 0 | 1 |
| 0 | nenulové | 0 | 1 |
| 0 | 0 | 0 | 0 |
Priorita operátorů
Pořadí, v jakém se budou jednotlivé části výrazu vyhodnocovat, můžeme podle potřeby zadat tím, že použijeme kulaté závorky pro ohraničení všech potřebných částí výrazu. Protože každý z výše uvedených operátorů má pevně dané pořadí vyhodnocování, není někdy závorek potřeba. Proto si nyní uvedeme pořadí vyhodnocování (prioritu) operátorů. Operátory v tabulce jsou seřazeny shora dolů podle klesající priority (tj. ty nejnižší se vyhodnocují nejpozději).
| symbol | poznámka | |
| 1. | () | závorky |
| 2. | .' .^ ' ^ | transpozice, umocnění, transpozice+konjugovanost, maticové umocnění |
| 3. | + - ~ | unární plus, unární minus, negace |
| 4. | .* ./ .\ * / \ | násobení po prvcích, dělení po prvcích, dělení po prvcích zleva, násobení matic, dělení matic, dělení matic zleva |
| 5. | + - | sčítání, odčítání |
| 6. | : | dvojtečka |
| 7. | < <= > >= == ~= | relační operátory |
| 8. | & | logický součin, AND |
| 9. | | | logický součet, OR |
Příklad:
výsledky jsou uvedeny pro a=-2; b=2; c=1.5 (protože se jedná o skaláry, tak není nutné používat operátory s tečkou):
| výraz | zápis v MATLABu | výsledek (zaokr. na 4 des. místa) |
|---|---|---|
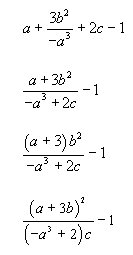 |
>> a+3*b^2/-a^3+2*c-1 | 1.5 |
>> (a+3*b^2)/(-a^3+2*c)-1 | -0.0909 | |
>> (a+3)*b^2/(-a^3+2*c)-1 | -0.6364 | |
>> (a+3*b)^2/((-a^3+2)*c)-1 | 0.0667 |
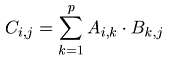
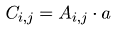
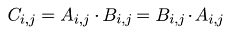
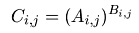 nebo
nebo 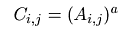 nebo
nebo