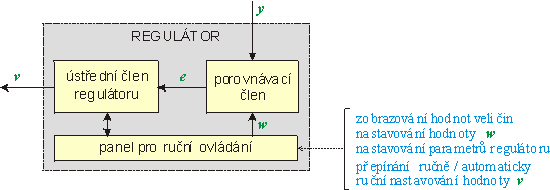
Obr. 3.19 Funkční schéma regulátoru
|
Obsah kapitoly: |
Jak již bylo řečeno, regulací rozumíme udržování určité technologické veličiny (tzv. regulovaná veličina) na určité, obvykle konstantní, hodnotě (tzv. řídicí veličina nebo žádaná hodnota). Regulátor je technické zařízení, které tuto funkci realizuje. Typů regulátorů existuje celá řada, můžeme je však rozdělit na dvě základní skupiny: regulátory pracující spojitě a regulátory pracující nespojitě. U spojitých regulátorů je vstupní i výstupní signál spojitou funkcí času, tj. může se měnit v každém časovém okamžiku, u nespojitých se vstup, výstup nebo obojí mění s časem nespojitě, tj. obvykle v určitém časovém okamžiku dochází ke skokové změně z jedné hodnoty na jinou, která se pak až do další skokové změny udržuje konstantní. V této kapitole se budeme zabývat spojitými regulátory, které jsou v praxi nejčastější. Moderní elektronické regulátory jsou sice svou podstatou nespojité, ale vzhledem k velice krátkým časovým intervalům mezi jednotlivými zásahy se navenek chovají prakticky jako spojité.
Na obr. 3.19 je znázorněno obecné funkční schéma regulátoru, které platí pro každý regulátor realizovaný jako samostatný technický prvek.
|
|
|
Obr. 3.19 Funkční schéma regulátoru |
Porovnávací člen určuje hodnotu regulační odchylky e odečtením měřené hodnoty regulované veličiny od hodnoty řídicí veličiny podle vztahu:
|
|
|
|
(3.6) |
Hodnota řídicí veličiny w se u běžných regulátorů buď nastavuje ručně na ovládacím panelu, nebo může být nastavována dálkově standardním signálem.
Regulační odchylku vypočtenou podle (3.6) zpracovává ústřední člen regulátoru a výsledkem je akční zásah, tedy signál ovládající akční člen. Funkce ústředního členu mohou být různé podle požadavků na kvalitu regulace. Z matematického hlediska je obecný tvar rovnice popisující chování (tj. časový průběh výstupu v) běžně užívaného spojitě pracujícího ústředního členu následující:
|
|
|
|
(3.7) |
Ústřední člen je tedy tvořen třemi částmi, které definují jeho vlastnosti:
· proporcionální složkou P, která určuje reakci regulátoru na velikost regulační odchylky; r0 je proporcionální konstanta (zesílení) regulátoru,
· integrační složkou I, která určuje reakci regulátoru na dobu trvání regulační odchylky; r-1 je integrační konstanta regulátoru,
· derivační složkou D, která určuje reakci regulátoru na rychlost změny hodnoty regulační odchylky, r1 je derivační konstanta regulátoru.
Dlouholetá praxe ukázala, že takto definované funkce ústředního členu regulátoru vyhovují v naprosté většině provozních aplikací. Konstrukční důvody regulátorů však vedly k tomu, že matematický popis musel být poněkud upraven do tvaru
|
|
|
|
(3.8) |
Jedná se o tzv. regulátor s interakcí, protože proporcionální konstantou r0 se násobí všechny tři členy rovnice. Konstanta Ti má rozměr času a je to tzv. integrační časová konstanta, konstanta Td má rovněž rozměr času a je to tzv. derivační časová konstanta. Konstanta r0 je opět zesílení regulátoru, ale v praxi se často setkáme s vyjádřením zesílení pomocí tzv. pásma proporcionality pp. Pásmo proporcionality udává, jak velká změna na vstupu regulátoru (e) v % způsobí 100 %-ní změnu na výstupu regulátoru (v). Vzájemný vztah mezi pp a r0 je tedy dán rovnicí
|
|
|
|
(3.7) |
Rovnice (3.7) a (3.8) popisují chování tzv. ideálních regulátorů, tj. takových, které reagují okamžitě, bez jakéhokoliv vlastního zpoždění. Moderní elektronické regulátory tuto podmínku prakticky splňují.
Výše uvedené tři základní vlastnosti ústředního členu se v reálných regulačních obvodech kombinují tak, aby regulace fungovala co nejlépe. Výsledné regulátory se pak označují příslušnou kombinací písmen P, I a D. V praxi se používají tyto typy regulátorů: P, PI, PD a PID. V následujícím přehledu jsou souhrnně uvedeny rovnice jejich chování a přenosové funkce (vždy bez interakce a s interakcí) a grafické znázornění odezvy výstupu na jednotkový skok regulační odchylky.
|
typ |
rovnice pro chování |
přenosová funkce |
odezva na skok na vstupu |
|
P |
|
|
|
|
|
|
||
|
PI |
|
|
|
|
|
|
||
|
PD |
|
|
|
|
|
|
||
|
PID |
|
|
|
|
|
|
U regulátorů s vlastností D se velikost derivační konstanty na grafu skokové odezvy neprojeví. Pro ně je v tomto teoretickém případě charakteristika v bodě t=0 nespojitá, protože derivace e je v okamžiku skoku nekonečně velká, v praxi to však v důsledku setrvačné hmoty akčního členu (např. ventilu) znamená jen tolik, že se otevře naplno a vzápětí vrátí zpět a dál se mění jeho poloha už pomalu.
| na začátek kapitoly |
S regulačním obvodem jsme se již seznámili. Na obr. 3.20 je nakresleno základní blokové schéma zpětnovazebního regulačního obvodu tvořeného regulovanou soustavou a regulátorem zapojeným ve zpětné vazbě. Dohromady tvoří zase systém, který má své dynamické vlastnosti.
|
|
|
Obr. 3.20 Blokové schéma zpětnovazebního regulačního obvodu |
Regulačním pochodem rozumíme celý proces probíhající v regulačním obvodu od okamžiku vzniku regulační odchylky až do okamžiku jejího odstranění regulátorem. Regulační pochod zpravidla zaznamenáváme graficky jako časovou závislost regulované veličiny. Regulovaná veličina se v praxi může odchýlit od své žádané hodnoty buď vlivem nějaké poruchy na vstupu regulované soustavy (hovoříme o reakci na poruchu), nebo v důsledku změny této žádané hodnoty (hovoříme o reakci na řízení).
|
|
|
Obr. 3.21 Záznam regulačního pochodu |
Na obr. 3.21 je zakreslen obecný průběh regulačního pochodu jako reakce na poruchu. Z grafu regulačního pochodu můžeme odečíst tyto z praktického hlediska důležité hodnoty:
· praktická doba regulace tr , což je doba od počátku regulačního pochodu až do chvíle, kdy hodnota regulované veličiny zůstane trvale v určeném intervalu kolem žádané hodnoty (v obrázku je označen D a volí se obvykle ±5% žádané hodnoty),
· maximální překmit ymax , tedy největší odchylka regulované veličiny od žádané hodnoty během regulačního pochodu,
· periodu kmitů Tk (jestliže je regulační pochod kmitavý),
· regulační plochu, což je integrál z regulační odchylky podle času
|
|
|
|
|
Každá z výše uvedených hodnot má svůj význam z hlediska posuzování vhodnosti průběhu regulačního pochodu vzhledem k požadavkům technologického procesu:
· praktická doba regulace určuje dobu po kterou bude regulační odchylka mimo určenou toleranci, tedy po kterou nebudou dodrženy požadované technologické podmínky,
· maximální překmit je třeba posuzovat např. z pohledu vzniku možné havarijní situace tím, že regulovaná veličina přestoupí na určitou dobu přípustnou mez,
· perioda kmitů má význam např. z hlediska přílišného zatěžování pohonu akčního členu častými změnami směru jeho chodu, nebo třeba z hlediska možného vzniku nestability chemické reakce probíhající v systému apod. ,
· regulační plocha v podstatě shrnuje všechna výše zmíněná kritéria a používá se k posuzování kvality regulačního pochodu hlavně v teorii regulace. Lepším a častěji užívaným kritériem než regulační plocha je integrál z druhé mocniny regulační odchylky podle času, protože eliminuje vliv znaménka regulační odchylky na hodnotu výsledku:
|
|
|
|
|
Obvykle požadujeme, aby po praktickém ukončení regulačního pochodu byla regulační odchylka v požadované toleranci kolem nuly. Regulační pochod však může někdy proběhnout aniž se dosáhlo tohoto stavu. Hovoříme pak o trvalé regulační odchylce, na kterou daný regulátor již vůbec nereaguje, nemění velikost akčního zásahu, a tudíž ji nemůže dále zmenšovat.
| na začátek kapitoly |
3.4.3 Volba typu regulátoru a nastavování jeho parametrů
Kvalitu regulace můžeme ovlivnit v podstatě dvojím způsobem: volbou typu regulátoru a nastavením jeho konstant. Je to v praxi vždycky práce pro odborníky, protože nekvalifikované zásahy mohou způsobit provozní problémy až havárii. Pro základní představu však uvedeme ty nejjednodušší zásady a postupy.
Volba typu regulátoru
Tuto volbu provádíme především podle požadavků technologického procesu. Již bylo řečeno, že z prakticky užívaných typů máme k dispozici regulátory s vlastnostmi P, PI, PD a PID. Pro konkrétní případ jednoduchého regulačního obvodu z nich vybíráme zhruba podle následujících zásad:
· P regulátor volíme pro méně náročné aplikace, kde nám nevadí trvalá regulační odchylka a preferujeme jednoduché a levné řešení,
· PI regulátor patří k nejběžněji používaným a volíme jej pro středně náročné aplikace, u kterých vyžadujeme, aby pracovaly bez trvalé regulační odchylky,
· PD regulátor se příliš často nepoužívá; co do trvalé regulační odchylky se chová stejně jako regulátor P, složka D však zesiluje jeho reakci na rychlost změny regulační odchylky, takže se uplatní při nepříliš náročné regulaci rychlých dějů,
· PID regulátor je vhodný pro náročné aplikace, pracuje bez trvalé regulační odchylky a je schopen dobře regulovat i rychlé děje.
V nedávné době vstupovala do rozhodování o volbě typu regulátoru jeho cena v mnohem větší míře než dnes, protože regulátory byly vyráběny buď jako mechanické přístroje (v kvalitě spadající do oblasti přesné mechaniky), nebo jako analogové elektronické obvody s vysokou přesností, linearitou a stabilitou. V současné době je naprostá většina komerční produkce regulátorů založena na mikroprocesorech a funkce regulátoru jsou dány programem, což se na konečné ceně projevuje jen málo. Většinou je to tak, že prodávaný regulátor je univerzálního typu PID a uživatel si sám nastavením jeho parametrů zvolí požadované vlastnosti. Pak namísto ceny vystupuje do popředí při volbě typu regulátoru skutečnost, že seřizování regulačního obvodu je tím složitější a choulostivější, čím více parametrů musíme nastavovat.
Nastavování parametrů regulátoru
Nastavování parametrů (tj. zesílení a časových konstant) regulátoru je záležitost poměrně složitá a měli by je provádět pouze odborníci. Vyžaduje to vždy znát dynamické chování soustavy, protože dynamické chování regulátoru se musí vlastnostem soustavy přizpůsobit tak, aby regulační pochod byl stabilní (to je nutná podmínka) a aby vykazoval takové chování, které technologický proces vyžaduje. Dnes se situace zjednodušila tím, že v řadě mikropočítačových regulátorů je zabudována funkce samočinného nastavování konstant („autotuning“). Regulátor v takovém případě vysílá do systému definované signály (akční zásahy) a sleduje odezvu na ně. Výsledek určitými matematickými postupy vyhodnocuje upravuje hodnoty svých parametrů. Algoritmy tohoto procesu nejsou jednoduché a bývají předmětem firemního tajemství. Pro ruční nastavování parametrů se často používají dvě poměrně jednoduché a v praxi ověřené metody:
· metoda podle Zieglera a Nicholse,
· metoda využívající experimentálně zjištěné odezvy soustavy na skokovou změnu akční veličiny.
Praktici často nastavují regulátory empiricky, to ale vyžaduje značnou zkušenost, cit pro to, jak velké změny hodnot parametrů je možné si dovolit v daném regulačním obvodu provádět a schopnost posoudit jejich účinek. Platí při tom zásada, že nejprve je nutné vyřadit integrační i derivační složku a nastavit pouze zesílení a pak teprve obvod dolaďovat přidáváním integrační a popřípadě derivační funkce, a to velmi opatrně. Jednodušší je to u regulátorů bez interakce, u regulátorů s interakcí je postup značně choulostivější.
| na začátek kapitoly |
3.4.4 Ukázky simulace regulačního pochodu
Ukázka R-3
Úkol:
Vytvořit simulační model PID regulátoru s interakcí (rov. 3.8) a zjistit odezvu jeho výstupy (v) na skokovou změnu vstupu (regulační odchylky e)
Řešení:
Jazyk PSI má k dispozici model regulátoru PI (blok PIC), ale nemá regulátor PID. Proto musíme model regulátoru sestavit podle rovnice (3.8) tak, že k bloku PIC přidáme derivační část využívající bloku DIF. Rovnici (3.8) upravíme na tvar:
|
|
|
|
Výstup skutečného regulátoru se vždy může pohybovat jen v určitých mezích daných použitým signálem. V praxi se obecně hovoří o rozmezí <0 %, 100 %> nebo <0, 1> a konkrétně tomu odpovídá patřičný normovaný signál, např. 4 - 20 mA. Proto také musíme do simulačního programu zabudovat toto omezení výstupu pomocí bloku LIM.
| Výpis programu: |
% Ukázka R-3 Simulace regulátoru PI vPI = PIC(e PAR:0.5,r0,Ti); % výstup části PI dere= DIF(e PAR:0); % derivace reg. odchylkyvD = r0*Td*dere; % výstup části Dv = LIM(vPI+vD PAR:0,1,1); % výstup PID s omezením na <0,1> r0 = 0.2; % zesíleníTi = 7; % časová integrační konstantaTd = 0.5; % časová derivační konstanta% jednotkový skok regulační odchylky v čase 5 e = BNG(time PAR:0,1,5); |
| Ukázka výsledků:
Počáteční hodnota výstupu je 0.5 (1.parametr bloku PIC). V okamžiku skoku regulační odchylky je vidět zákmit vlivem derivační složky a pak stoupání výstupu vlivem integrační složky. V místě křížku začal fungovat blok LIM a nedovolil, aby výstup překročil hodnotu 1.
|
|
|
Program v PSI: |
soubory: Ukaz_R-3.PSM , Ukaz_R-3.MOD |
V programu je možné měnit hodnoty parametrů regulátoru a sledovat jejich vliv na výstup, je možné změnit i znaménko skoku regulační odchylky apod.
| na začátek kapitoly |
Ukázka R-4
Úkol:
Vytvořit simulační model regulačního obvodu, kde regulovanou soustavou je model ohřívače vody (příklad M-1) a kde je použito regulátoru PI. Model je kvůli kapacitě demoverze PSI poněkud zjednodušen (je vypuštěna účinnost topení) a je popsán rovnicí
|
|
|
Příkon topení je možné měnit spojitě od 0 do 100 000 podle výstupu z regulátoru, který je omezen na <0, 1>. Počáteční hodnota teploty T2 = , což odpovídá ustálenému stavu, výstup z regulátoru je nastaven tak, aby příkon topení v ustáleném stavu byl 60 000 .
| Výpis programu: |
% Ukázka R-4 (regulace teploty na výstupu ohřívače vody) % regulovaná soustava T2 = INT((Q*(T1-T2)+P*k)/5 PAR:40); % teplota na výstupu k = 2.388e-4; % konstanta k P = v*100000; % ovládání příkonu topení regulátorem T1 = 15; % teplota vody na vstupu Q = BNG(time PAR:0.5,0.4,5); % porucha - skok průtoku vody % regulátor Tw = 40; % žádaná hodnota teploty e = Tw-T2; % regulační odchylka vreg= PIC(e PAR: 0.524,0.3,7); % regulátor PI v = LIM(vreg PAR:0,1,1); % omezení výstupu regulátoru |
| Ukázka výsledků:
regulátor P, odezva na poruchu Q (z 0.5 na 0.4 l/min), zůstává trvalá regulační odchylka (v čase simulace 50 min je odchylka -0.33 °C)
Poznámka: |
|
|
regulátor PI, odezva na poruchu Q z 0.5 na 0.4 l/min), trvalá regulační odchylka je odstraněna (v čase simulace 50 min je odchylka -0.00067 °C)
|
|
| Je možné měnit zesílení a časovou integrační konstantu regulátoru a zkoušet vliv jejich hodnot na průběh regulačního pochodu. Tyto simulace ukazují, jak regulační obvod reaguje na poruchu. V řadě aplikací, kde se často mění žádaná hodnota, je důležité, aby regulační obvod uspokojivě reagoval i na tuto změnu (tzv. změnu řízení). Takovou odezvu pro náš příklad ukazuje následující simulace, kdy se Tw mění v čase 5 minut (program k tomu účelu byl upraven tak, že hodnota Tw je simulována blokem BNG a Q zůstává konstantní). | |
|
regulátor PI, odezva na změnu řízení (ze 40 na 45 °C), regulační odchylka od nové žádané hodnoty je vyhovující (v čase simulace 50 min je odchylka -0.007 °C) 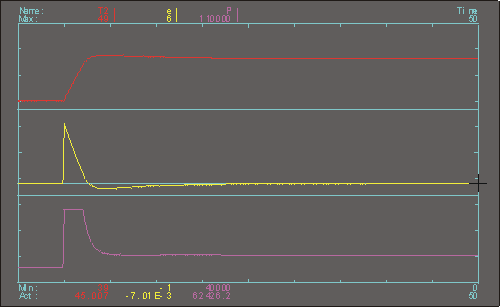 |
|
|
Program v PSI: |
soubory: Ukaz_R-4.PSM , Ukaz_R-4.MOD |
| na začátek kapitoly |